
|
Cococubed.com
|
|
Effective reaction rates for reaction networks |
Home
Astronomy Research
2026 Neutrinos From De-excitation
2024 Radiative Opacity
2024 Neutrino Emission from Stars
2023 White Dwarfs & 12C(α,γ)16O
2023 MESA VI
2022 Earendel, A Highly Magnified Star
2022 Black Hole Mass Spectrum
2021 Skye Equation of State
2021 White Dwarf Pulsations & 22Ne
Software Instruments
2026 AAS Journals
AAS YouTube
Listing of 500+ Author Videos
AAS Peer Review Workshops
Outreach Material
Education Material
Other Stuff:
Bicycle Adventures
Illustrations
Presentations
Contact: F.X.Timmes
my one page vitae,
full vitae,
research statement, and
teaching statement.
$ \def\drvop#1{{\frac{d}{d{#1}}}} \def\drvf#1#2{{\frac{d{#1}}{d{#2}}}} \def\ddrvf#1#2{{\frac{d^2{#1}}{d{#2}^2}}} \def\partop#1{{\frac{\partial}{\partial {#1}}}} \def\ppartop#1{{\frac{\partial^2}{\partial {#1}^2}}} \def\partf#1#2{{\frac{\partial{#1}}{\partial{#2}}}} \def\ppartf#1#2{{\frac{\partial^2{#1}}{\partial{#2}^2}}} \def\mpartf#1#2#3{{\frac{\partial^2{#1}}{\partial{#2} \ {\partial{#3}}}}} $ A pdf of this note is avaliable.
In this note we show how reaction sequences may, under steady state assumptions, be replaced with a simpler reaction sequence and an effective rate. These techniques are widely used in hardwired approximation reaction networks. The aim is to reduce the number of isotopes evolved in a reaction network, and thus the execution time of an implicit integration. The cost is a more complicated Jacobian matrix as the effective reaction rates depend on the abundances.
($\alpha$,p)(p,$\gamma$) sequences
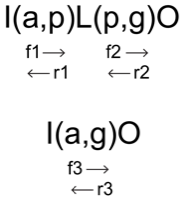
Consider the reaction sequence I(a,p)L(p,g)O
|
where I(a,p)L occurrs in the forward direction with a reaction rate f$_1$ and a reverse reaction rate r$_1$. Similarly, L(p,g)O occurs in the forward direction with a reaction rate f$_2$ and a reverse reaction rate r$_2$. The goal is to reduce the sequence I(a,p)L(p,g)O to the sequence I(a,g)O with an effective forward, f$_3$, and effective reverse, r$_3$, reaction rate such the that species L does not need to be included in the reaction network.
Writing out all the terms associated with the full reaction sequence \begin{align} \dot{Y}(I) & = - Y(I) \ Y(a) \ f_1 + Y(p) \ Y(L) \ r_1 \label{1} \tag{1} \\ \dot{Y}(a) & = - Y(I) \ Y(a) \ f_1 + Y(p) \ Y(L) \ r_1 \label{2} \tag{2} \\ \dot{Y}(p) & = + Y(I) \ Y(a) \ f_1 - Y(p) \ Y(L) \ r_1 - Y(L) \ Y(p) \ f_2 + Y(O) \ r_2 \label{3} \tag{3} \\ \dot{Y}(L) & = + Y(I) \ Y(a) \ f_1 - Y(p) \ Y(L) \ r_1 - Y(L) \ Y(p) \ f_2 + Y(O) \ r_2 \label{4} \tag{4} \\ \dot{Y}(O) & = + Y(L) \ Y(p) \ f_2 - Y(O) \ r_2 \label{5} \tag{5} \ . \end{align} Assume $\dot{Y}(L) = 0$ so that the abundance of $Y(L)$ is in steady state. In this specific case, $\dot{Y}(L) = 0$ also means $\dot{Y}(p) = 0$, so a proton abundance does not need to be evolved either. Rearranging equation ($\ref{4}$), \begin{equation} Y(I) \ Y(a) \ f_1 + Y(O) \ r_2 = Y(p) \ Y(L) \ r_1 + Y(L) \ Y(p) \ f_2 \ . \label{6} \tag{6} \end{equation} Solving for $Y(p)Y(L)$ \begin{equation} Y(p) Y(L) = \frac{Y(I) \ Y(a) \ f_1 + Y(O) \ r_2}{ r_1 + f_2} \ . \label{7} \tag{7} \end{equation} Let \begin{equation} v = \frac{r_1}{r_1 + f_2} \ . \label{8} \tag{8} \end{equation} Note that \begin{equation} \frac{r_1}{r_1 + f_2} + \frac{f_2}{r_1 + f_2} = 1 \label{9} \tag{9} \end{equation} or \begin{equation} \frac{f_2}{r_1 + f_2} = 1 - v \ . \label{10} \tag{10} \end{equation} Substituting equations ($\ref{7}$) and ($\ref{8}$) into equation ($\ref{1}$) \begin{align} \dot{Y}(I) & = - Y(I) \ Y(a) \ f_1 + Y(p) \ Y(L) \ r_1 \\ & = - Y(I) \ Y(a) \ f_1 + \left [\frac{Y(I) \ Y(a) \ f_1 + Y(O) \ r_2}{ r_1 + f_2} \right ] \ r_1 \\ & = - Y(I) \ Y(a) \ f_1 + [Y(I) \ Y(a) \ f_1 + Y(O) \ r_2] \ v \\ & = - Y(I) \ Y(a) \ f_1 \ (1 - v) + Y(O) \ r_2 \ v \tag{11} \ . \end{align} This identifies the effective reaction rates f$_3$ and r$_3$ as \begin{align} f_3 & = f_1 \ (1 - v) = \frac{f_1 \cdot f_2}{r_1 + f_2} \\ r_3 & = r_2 \ v = \frac{r_1 \cdot r_2}{r_1 + f_2} \ , \tag{12} \end{align} and we have the desired final form \begin{equation} \dot{Y}(I) = - Y(I) \ Y(a) \ f_3 + Y(O) \ f_3 \ . \label{13} \tag{13} \end{equation} Since the ODE for $Y(a)$ is identical to that for $Y(I)$, \begin{equation} \dot{Y}(a) = - Y(I) \ Y(a) \ f_3 + Y(O) \ r_3 \ . \label{14} \tag{14} \end{equation} Substituting equations ($\ref{7}$) and ($\ref{8}$) into equation ($\ref{5}$) gives the ODE for $Y(O)$ \begin{align} \dot{Y}(O) & = Y(L) \ Y(p) \ f_2 - Y(O) \ r_2 \\ & = \left [\frac{Y(I) \ Y(a) \ f_1 + Y(O) \ r_2}{ r_1 + f_2} \right ] \ f_2 - Y(O) \ r_2 \\ & = [Y(I) \ Y(a) \ f_1 + Y(O) \ r_2] \ (1 -v) - Y(O) \ r_2 \\ & = Y(I) \ Y(a) \ f_1 (1 -v) - Y(O) \ r_2 \ v \\ & = Y(I) \ Y(a) \ f_3 - Y(O) \ r_3 \label{15} \tag{15} \ . \end{align}
Equations ($\ref{13}$), ($\ref{14}$), and ($\ref{15}$) constitute the simpler sequence I(a,g)O with a effective forward, f$_3$, and an effective reverse, r$_3$, reaction rate such the that species L or p does not need to be included in the reaction network.
Some limits. Note that $v \rightarrow 0$ when $f_2 >> r_1$. This means the (p,g) reaction rate is much stronger than the (p,a) reaction rate, allowing strong flows to species O. The ODEs reduce to \begin{align} \dot{Y}(I) & = - Y(I) \ Y(a) \ f_1 \notag \\ \dot{Y}(a) & = - Y(I) \ Y(a) \ f_1 \tag{16} \\ \dot{Y}(O) & = + Y(I) \ Y(a) \ f_1 \notag \end{align} as expected. Similarily, $v \rightarrow 1$ when $r_1 >> f_2$, meaning the (p,a) reaction rate is much stronger than the (p,g) reaction rate and thus inhibiting flows to species O. The ODEs reduce to \begin{align} \dot{Y}(I) & = + Y(O) \ r_2 \notag \\ \dot{Y}(a) & = + Y(O) \ r_2 \tag{17} \\ \dot{Y}(O) & = - Y(O) \ r_2 \notag \label{eq:odes_limit2} \end{align} as expected.
Similar expressions hold for (a,n)(n,g) sequences with the obvious replacement of Y(n) for Y(p) in equations ($\ref{13}$), ($\ref{14}$), and ($\ref{15}$).
(n,$\gamma$)(n,$\gamma$) sequences
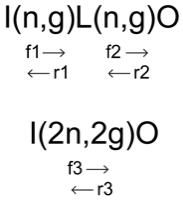
Consider the reaction sequence I(n,g)L(n,g)O
|
As above, the goal is to reduce the sequence I(n,g)L(n,g)O to the simpler sequence I(2n,2g)O with an effective forward rate f$_3$ and an effective reverse rate r$_3$ such the that species L does not need to be included in the reaction network. Writing out all the terms associated with the full reaction sequence \begin{align} \dot{Y}(I) & = - Y(I) \ Y(n) \ f_1 + Y(L) \ r_1 \label{18} \tag{18}\\ \dot{Y}(n) & = - Y(I) \ Y(n) \ f_1 + Y(L) \ r_1 - Y(L) \ Y(n) \ f_2 + Y(O) \ r_2 \label{19} \tag{19} \\ \dot{Y}(L) & = + Y(I) \ Y(n) \ f_1 - Y(L) \ r_1 - Y(L) \ Y(n) \ f_2 + Y(O) \ r_2 \label{20} \tag{20} \\ \dot{Y}(O) & = + Y(L) \ Y(n) \ f_2 - Y(O) \ r_2 \label{21} \tag{21} \ . \end{align} Assume $\dot{Y}(L) = 0$ so that the abundance of $Y(L)$ is in steady state. Rearranging equation ($\ref{20}$) \begin{equation} Y(L) \ Y(n) \ f_2 +Y(L) \ r_1 = Y(I) \ Y(n) \ f_1 + Y(O) \ r_2 \ . \label{22} \tag{22} \end{equation} Solving for $Y(L)$ \begin{equation} Y(L) = \frac{Y(I) \ Y(n) \ f_1 + Y(O) \ r_2}{ r_1 + Y(n) \ f_2} \ . \label{23} \tag{23} \end{equation} Let \begin{equation} v = \frac{r_1}{r_1 + Y(n) \ f_2} \ , \label{24} \tag{24} \end{equation} which implies \begin{equation} \frac{r_1}{r_1 + Y(n) \ f_2} + \frac{Y(n) \ f_2}{r_1 + Y(n) \ f_2} = 1 \label{25} \tag{25} \end{equation} or \begin{equation} \frac{Y(n) \ f_2}{r_1 + Y(n)\ f_2} = 1 - v \ . \label{26} \tag{26} \end{equation} Substituting equations ($\ref{23}$) and ($\ref{24}$) into equation ($\ref{18}$) \begin{align} \dot{Y}(I) & = - Y(I) \ Y(n) \ f_1 + Y(L) \ r_1 \notag \\ & = - Y(I) \ Y(n) \ f_1 + \left [\frac{Y(I) \ Y(n) \ f_1 + Y(O) \ r_2}{ r_1 + Y(n) \ f_2} \right ] \ r_1 \notag \\ & = - Y(I) \ Y(n) \ f_1 + [Y(I) \ Y(n) \ f_1 + Y(O) \ r_2] \ v \notag \\ & = - Y(I) \ Y(n) \ f_1 \ (1 - v) + Y(O) \ r_2 \ v \label{27} \tag{27} \ . \end{align} This identifies the effective reaction rates f$_3$ and r$_3$ as \begin{align} f_3 & = f_1 \ (1 - v) = \frac{f_1 \cdot Y(n)\ f_2}{r_1 + Y(n) \ f_2} \notag \\ r_3 & = r_2 \ v = \frac{r_1 \cdot r_2}{r_1 + Y(n) \ f_2} \label{28} \tag{28} \ , \end{align} and we have the desired final form \begin{equation} \dot{Y}(I) = - Y(I) \ Y(n) \ f_3 + Y(O) \ r_3 \ . \label{29} \tag{29} \end{equation} Similarly for evolution of $Y(O)$ in equation ($\ref{21}$), \begin{align} \dot{Y}(O) & = Y(L) \ Y(n) \ f_2 - Y(O) \ r_2 \notag \\ & = \left [\frac{Y(I) \ Y(n) \ f_1 + Y(O) \ r_2}{ r_1 + Y(n) \ f_2} \right ] \ Y(n) \ f_2 - Y(O) \ r_2 \notag \\ & = [Y(I) \ Y(n) \ f_1 + Y(O) \ r_2] \ (1 -v) - Y(O) \ r_2 \notag \\ & = Y(I) \ Y(n) \ f_1 (1 -v) - Y(O) \ r_2 \ v \notag \\ & = Y(I) \ Y(n) \ f_3 - Y(O) \ r_3 \label{30} \tag{30} \ . \end{align} And for the neutron abundance of equation ($\ref{19}$) \begin{align} \dot{Y}(n) & = - Y(I) \ Y(n) \ f_1 + Y(L) \ r_1 - Y(L) \ Y(n) \ f_2 + Y(O) \ r_2 \notag \\ & = - Y(I) \ Y(n) \ f_1 + \left [ \frac{Y(I) \ Y(n) \ f_1 + Y(O) \ r_2}{ r_1 + Y(n) \ f_2} \right ] \ r_1 \notag \\ &\phantom{{}={}} - \left [ \frac{Y(I) \ Y(n) \ f_1 + Y(O) \ r_2}{ r_1 + Y(n) \ f_2} \right ] Y(n) \ f_2 + Y(O) \ r_2 \notag \\ & = - Y(I) \ Y(n) \ f_1 + [Y(I) \ Y(n) \ f_1 + Y(O) \ r_2] \ v \notag \\ &\phantom{{}={}} - [Y(I) \ Y(n) \ f_1 + Y(O) \ r_2] \ (1-v) - Y(O) \ r_2 \notag \\ & = -2\ Y(I) \ Y(n) \ f_2 \ (1 - v) + 2 Y(O) \ r_2 \ v \notag \\ & = -2\ Y(I) \ Y(n) \ f_3 + 2 Y(O) \ r_3 \label{31} \tag{31} \ . \end{align} Equations ($\ref{29}$), ($\ref{30}$), and ($\ref{31}$) constitute the simpler sequence I(2n,2g)O with a effective forward rate, f$_3$, and an effective reverse rate, r$_3$, such the that species L does not need to be included in the reaction network. Similar expressions hold for (p,g)(p,g) sequences with the obvious replacement of $Y(p)$ for $Y(n)$ in equations ($\ref{29}$), ($\ref{30}$), and ($\ref{31}$).
($\alpha$,p)($\gamma$,p) sequences
Finally, consider the reaction sequence I(a,p)L(g,p)O, which has less symmetry than the previous two cases. As before, the goal is to reduce this sequence to the simpler sequence I(a,2p)O with an effective forward, f$_3$, and effective reverse, r$_3$, reaction rate such the that species L does not need to be included in the reaction network.
Writing out all the terms associated with the full reaction sequence \begin{align} \dot{Y}(I) & = - Y(I) \ Y(a) \ f_1 + Y(L) \ Y(p) \ r_1 \label{32} \tag{32} \\ \dot{Y}(a) & = - Y(I) \ Y(a) \ f_1 + Y(L) \ Y(p) \ r_1 \label{33} \tag{33} \\ \dot{Y}(p) & = + Y(I) \ Y(a) \ f_1 - Y(L) \ Y(p) \ r_1 + Y(L) \ f_2 - Y(O) \ Y(p) \ r_2 \label{34} \tag{34} \\ \dot{Y}(L) & = + Y(I) \ Y(a) \ f_1 - Y(L) \ Y(p) \ r_1 - Y(L) \ f_2 + Y(O) \ Y(p) \ r_2 \label{35} \tag{35} \\ \dot{Y}(O) & = + Y(L) \ f_2 - Y(O) \ Y(p) \ r_2 \label{36} \tag{36} \ . \end{align} Assuming $\dot{Y}(L) = 0$ so that $Y(L)$ is in steady state. Rearranging equation ($\ref{35}$) \begin{equation} Y(I) \ Y(a) \ f_1 + Y(O) \ Y(p) \ r_2 = Y(L) \ Y(p) \ r_1 + Y(L) \ f_2 \ . \label{37} \tag{37} \end{equation} Solving for $Y(L)$ \begin{equation} Y(L) = \frac{Y(I) \ Y(a) \ f_1 + Y(O) \ Y(p) \ r_2}{ f_2 + Y(p) \ r_1} \ . \label{38} \tag{38} \end{equation} Let \begin{equation} v = \frac{Y(p) \ r_1}{f_2 + Y(p) \ r_1} \label{39} \tag{39} \ . \end{equation} This definition implies \begin{equation} \frac{Y(p) \ r_1}{f_2 + Y(p) \ r_1} + \frac{f_2}{f_2 + Y(p) \ r_1} = 1 \label{40} \tag{40} \end{equation} or \begin{equation} \frac{f_2}{f_2 + Y(p)\ r_1} = 1 - v \ . \label{41} \tag{41} \end{equation} Substituting equations ($\ref{38}$) and ($\ref{39}$) into ($\ref{32}$) \begin{align} \dot{Y}(I) & = - Y(I) \ Y(a) \ f_1 + Y(L) \ Y(p) \ r_1 \notag \\ & = - Y(I) \ Y(a) \ f_1 + \left [\frac{Y(I) \ Y(a) \ f_1 + Y(O) \ Y(p) \ r_2}{ f_2 + Y(p) \ r_1} \right ] \ r_1 \notag \\ & = - Y(I) \ Y(a) \ f_1 + [Y(I) \ Y(a) \ f_1 + Y(O) \ Y(p) \ r_2] \ v \notag \\ & = - Y(I) \ Y(a) \ f_1 \ (1 - v) + Y(O) \ Y(p) \ r_2 \ v \label{42} \tag{42} \ . \end{align} This identifies the effective reaction rates f$_3$ and r$_3$ as \begin{align} f_3 & = f_1 \ (1 - v) = \frac{f_1 f_2}{f_2 + Y(p) \ r_1} \notag \\ r_3 & = r_2 \ v = \frac{Y(p) \ r_1 \ r_2}{f_2 + Y(p) \ r_1} \label{43} \tag{43} \ , \end{align} and we have the desired final forms \begin{align} \dot{Y}(I) & = - Y(I) \ Y(a) \ f_3 + Y(O) \ Y(p) \ r_3 \label{44} \tag{44} \\ \dot{Y}(a) & = - Y(I) \ Y(a) \ f_3 + Y(O) \ Y(p) \ r_3 \label{45} \tag{45} \\ \dot{Y}(O) & = Y(I) \ Y(a) \ f_3 - Y(O) \ Y(p) \ r_3 \label{46} \tag{46} \\ \dot{Y}(p) & = 2\ Y(I) \ Y(a) \ f_3 - 2 Y(O) \ Y(p) \ r_3 \label{47} \tag{47} \ . \end{align} which constitute the simpler sequence I(a,2p)O with a effective forward, f$_3$, and an effective reverse, r$_3$, reaction rate such the that species L does not need to be included in the reaction network.
Similar expressions hold for (a,n)(g,n) sequences with the obvious replacement of Y(n) for Y(p).