|
Cococubed.com
|
| SN 1987A Light Curve |
Home
Astronomy research
Software Infrastructure:
MESA
FLASH-X
STARLIB
MESA-Web
starkiller-astro
My instruments
Neutrino Emission:
De-excitation Neutrinos
Neutrino emission from stars
Identifying the Pre-SN
Neutrino HR diagram
Pre-SN Beta Processes
Pre-SN neutrinos
White dwarf pulsations:
12C(α,γ) & overshooting
Probe of 12C(α,γ)16O
Impact of 22Ne
Impact of ν cooling
Variable white dwarfs
MC reaction rates
Micronovae
Novae
White dwarf supernova:
Stable nickel production
Remnant metallicities
Colliding white dwarfs
Merging white dwarfs
Ignition conditions
Metallicity effects
Central density effects
Detonation density
Tracer particle burning
Subsonic burning fronts
Supersonic fronts
W7 profiles
Massive stars:
Pop III with HST/JWST
Rotating progenitors
3D evolution to collapse
MC reaction rates
Pre-SN variations
Massive star supernova:
Yields of radionuclides
26Al & 60Fe
44Ti, 60Co & 56Ni
SN 1987A light curve
Constraints on Ni/Fe
An r-process
Effects of 12C +12C
Neutron Stars and Black Holes:
Black Hole spectrum
Mass Gap with LVK
Compact object IMF
He burn neutron stars
Stars:
Hypatia catalog
SAGB stars
Nugrid Yields I
He shell convection
BBFH at 40 years
γ-rays within 100 Mpc
Iron Pseudocarbynes
Pre-Solar Grains:
C-rich presolar grains
SiC Type U/C grains
Grains from massive stars
Placing the Sun
SiC Presolar grains
Chemical Evolution:
Radionuclides in 2020s
Zone models H to Zn
Mixing ejecta
Thermodynamics, Opacities & Networks
Radiative Opacity
Skye EOS
Helm EOS
Five EOSs
Equations of State
12C(α,γ)16O Rate
Proton-rich NSE
Reaction networks
Bayesian reaction rates
Verification Problems:
Validating an astro code
Su-Olson
Cog8
Mader
RMTV
Sedov
Noh
Software Instruments
AAS Journals
2025 AAS YouTube
2025 AAS Peer Review Workshops
2025 ASU Energy in Everyday Life
2025 MESA Classroom
Other Stuff:
Bicycle Adventures
Illustrations
Presentations
Contact: F.X.Timmes
my one page vitae,
full vitae,
research statement, and
teaching statement.
In this article, we revisit the evidence for the contribution of the long-lived radioactive nuclides $^{44}$Ti, $^{55}$Fe, $^{56}$Co, $^{57}$Co, and $^{60}$Co to the UVOIR light curve of SN 1987A.
We show that the V-band luminosity constitutes a roughly constant fraction of the bolometric luminosity between 900 and 1900 days, and we obtain an approximate bolometric light curve out to 4334 days by scaling the late time V-band data by a constant factor where no bolometric light curve data is available. Considering the five most relevant decay chains starting at $^{44}$Ti, $^{55}$Co, $^{56}$Ni, $^{57}$Ni, and $^{60}$Co, we perform a least squares fit to the constructed composite bolometric light curve. For the nickel isotopes, we obtain best fit values of M($^{56}$Ni) = (7.1 $\pm$ 0.3) × 102 M⊙ and M($^{57}$Ni) = (4.1 $\pm$ 1.8) × 10-3 M⊙. Our best fit $^{44}$Ti mass is M($^{44}$Ti) = (0.55 $\pm$ 0.17) × 10-4 M⊙. which is in disagreement with the much higher (3.1 $\pm$ 0.8) × 10-4 M⊙ recently derived from INTEGRAL observations. The half-lives of $^{60}$Co and $^{55}$Fe are quite similar, which introduces a degeneracy for the fitting algorithm. As a result, we can only give upper limits on the relevant production masses of M($^{55}$Co) < 7.2 × 10-3 M⊙ and M($^{60}$Co) < 1.7 × 10-4 M⊙. Furthermore, we find that the leptonic channels in the decay of $^{57}$Co (internal conversion and Auger electrons) are a significant contribution and constitute up to 15.5% of the total luminosity. Consideration of the kinetic energy of these electrons is essential in lowering our best fit nickel isotope production ratio to [$^{57}$Ni / $^{56}$Ni] = 2.5$\pm$1.1 which is still somewhat high but in agreement with gamma-ray observations and model predictions.
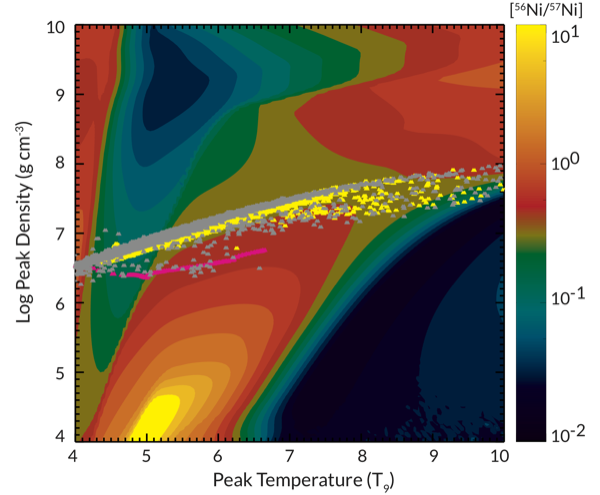
[57Ni / 56Ni] after freeze-out |
|
For canonically accepted values |
Including freeze-out corrections |
Importance of 57Co |
Best fit |