
|
Cococubed.com
|
| Electron and Positron Chemical Potentials |
Home
Astronomy Research
2025 Neutrinos From De-excitation
Radiative Opacity
2024 Neutrino Emission from Stars
2023 White Dwarfs & 12C(α,γ)16O
2023 MESA VI
2022 Earendel, A Highly Magnified Star
2022 Black Hole Mass Spectrum
2021 Skye Equation of State
2021 White Dwarf Pulsations & 22Ne
Software Instruments
Stellar equation of states
EOS with ionization
EOS for supernovae
Chemical potentials
Stellar atmospheres
Voigt Function
Jeans escape
Polytropic stars
Cold white dwarfs
Adiabatic white dwarfs
Cold neutron stars
Stellar opacities
Neutrino energy loss rates
Ephemeris routines
Fermi-Dirac functions
Polyhedra volume
Plane - cube intersection
Coating an ellipsoid
Nuclear reaction networks
Nuclear statistical equilibrium
Laminar deflagrations
CJ detonations
ZND detonations
Fitting to conic sections
Unusual linear algebra
Derivatives on uneven grids
Pentadiagonal solver
Quadratics, Cubics, Quartics
Supernova light curves
Exact Riemann solutions
1D PPM hydrodynamics
Hydrodynamic test cases
Galactic chemical evolution
Universal two-body problem
Circular and elliptical 3 body
The pendulum
Phyllotaxis
MESA
MESA-Web
FLASH
Zingale's software
Brown's dStar
GR1D code
Iliadis' STARLIB database
Herwig's NuGRID
Meyer's NetNuc
AAS Journals
2025 AAS YouTube
2025 Listing of 500+ Author Videos
2025 AAS Peer Review Workshops
2025 ASU Energy in Everyday Life
2025 MESA Classroom
Other Stuff:
Bicycle Adventures
Illustrations
Presentations
Contact: F.X.Timmes
my one page vitae,
full vitae,
research statement, and
teaching statement.
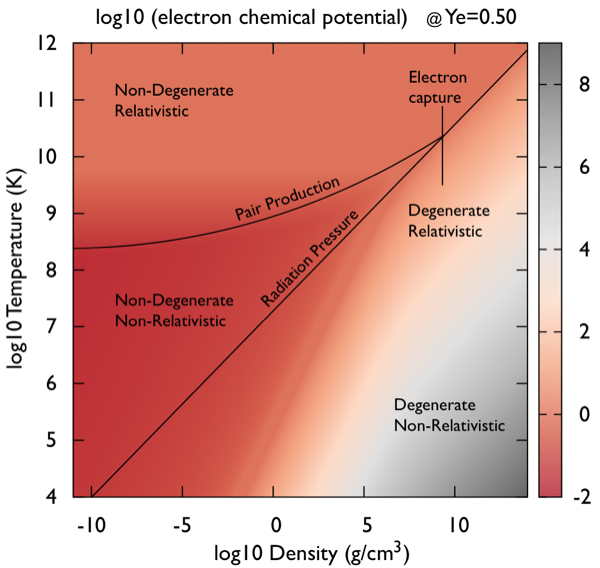
|
The tool in
chem_poten.tbz
returns the electron and positron chemical
potentials as a function of temperature, density and Ye
for a fully ionized stellar plasma.
The electron chemical potentials returned do not include the electron rest mass, so the value returned is the "kinetic chemical potential". This means that the positron chemical potential must have the rest-mass terms appear explicitly, ηpos = -ηele - 2mec2. One can see this being applied at the end of the relevant routine. This tool is derived from the Helmholtz equation of state. A stand-alone electron/positron chemical potential solver may be useful for Compton opacities (e.g., Poutanen 2017) weak reaction rates, reaction rate screening factors, and others where invoking the full machinery of an equation of state may not be as desirable. |
Ten tips about the chemical potential (from Peter Saeta)
- It expresses how eager a system is for particles.
- In equilibrium it is equal in two systems placed in diffusive contact.
- Particles move from a region of high chemical potential to a region of low chemical potential.
- It can be found by differentiating thermodynamic potentials with respect to N.
- It has an internal part and an external part; the external part is just a normal per-particle potential energy, such as mgh.
- It is the Gibbs free energy per particle, G/N.
- It is used to describe chemical equilibria.
- For a monatomic ideal gas, it is kT ln (νQ/ν).
- It is enormously useful in describing equations of state.
- It is the factor you use to get the particle number right!
Number 10 is probably the most pragmatic. In the tool chem_poten.tbz, one balances the number density of electrons from fully ionized material with the net number density of electrons and positrons coming from the relevant Fermi-Dirac statistics.