Cococubed.com Thermal Escape
Home Astronomy Research    2025 Neutrinos From De-excitation    Radiative Opacity    2024 Neutrino Emission from Stars    2023 White Dwarfs & 12C(α,γ)16O    2023 MESA VI    2022 Earendel, A Highly Magnified Star    2022 Black Hole Mass Spectrum    2021 Skye Equation of State    2021 White Dwarf Pulsations & 22Ne    Software Instruments      Stellar equation of states      EOS with ionization      EOS for supernovae      Chemical potentials      Stellar atmospheres      Voigt Function      Jeans escape      Polytropic stars      Cold white dwarfs      Adiabatic white dwarfs      Cold neutron stars      Stellar opacities      Neutrino energy loss rates      Ephemeris routines      Fermi-Dirac functions      Polyhedra volume      Plane - cube intersection      Coating an ellipsoid      Nuclear reaction networks      Nuclear statistical equilibrium      Laminar deflagrations      CJ detonations      ZND detonations      Fitting to conic sections      Unusual linear algebra      Derivatives on uneven grids      Pentadiagonal solver      Quadratics, Cubics, Quartics      Supernova light curves      Exact Riemann solutions      1D PPM hydrodynamics      Hydrodynamic test cases      Galactic chemical evolution      Universal two-body problem      Circular and elliptical 3 body      The pendulum      Phyllotaxis      MESA      MESA-Web      FLASH      Zingale's software      Brown's dStar      GR1D code      Iliadis' STARLIB database      Herwig's NuGRID      Meyer's NetNuc AAS Journals    2025 AAS YouTube    2025 AAS Peer Review Workshops 2025 ASU Energy in Everyday Life 2025 MESA Classroom Other Stuff:    Bicycle Adventures    Illustrations    Presentations Contact: F.X.Timmes my one page vitae, full vitae, research statement, and teaching statement.	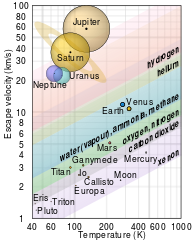Given a planet's mass ${\rm M}$, radius ${\rm R}$, and the height of its exosphere ${\rm h}$ at temperature ${\rm T}$, the thermal escape timescale $\tau_{\rm escape}$ for an atom/molecule of mass ${\rm m}$ can be estimated from $$ {\rm \tau_{escape} = \dfrac{H}{v_{jeans}} } \label{eq1} \tag{1} $$ where the scale height ${\rm H}$ and acceleration due to gravity ${\rm g}$ are $$ {\rm H =\dfrac{k \ T}{m \ g} } \qquad \qquad {\rm g = \dfrac{G \ M} {(R + h)^2} } \label{eq2} \tag{2} $$ and the Jeans speed ${\rm v_{Jeans}}$ is $$ {\rm v_{jeans} = v_{{\rm peak}} \dfrac{(1+ \lambda) \ e^{-\lambda}}{\sqrt{4 \pi}} } \ . \label{eq3} \tag{3} $$ The peak speed ${\rm v_{peak}}$, escape speed ${\rm v_{escape}}$, and their ratio $\lambda$ are $$ {\rm v_{peak} = \sqrt{\dfrac{2 k T}{m}} } \qquad \qquad {\rm v_{escape} = \sqrt {\dfrac{2 G M}{R + h}} } \qquad \qquad {\rm \lambda = \left ( \dfrac{ v_{escape}}{v_{peak}} \right )^2 } \label{eq4} \tag{4} $$ The tool contained in public_jeans_escape.tbz implements these simple analytic formulas along with comparing their results to numerical integrations of the Maxwell-Boltzmann distribution. Here are the speed distributions for hydrogen helium, carbon, nitrogen, and oxygen for Earth's exosphere and their associated thermal escape timescales.
	Please cite the relevant references if you publish a piece of work that use these codes, pieces of these codes, or modified versions of them. Offer co-authorship as appropriate.