Cococubed.com Thermal Neutrino Loss Rates
Home Astronomy Research    2025 Neutrinos From De-excitation    Radiative Opacity    2024 Neutrino Emission from Stars    2023 White Dwarfs & 12C(α,γ)16O    2023 MESA VI    2022 Earendel, A Highly Magnified Star    2022 Black Hole Mass Spectrum    2021 Skye Equation of State    2021 White Dwarf Pulsations & 22Ne    Software Instruments      Stellar equation of states      EOS with ionization      EOS for supernovae      Chemical potentials      Stellar atmospheres      Voigt Function      Jeans escape      Polytropic stars      Cold white dwarfs      Adiabatic white dwarfs      Cold neutron stars      Stellar opacities      Neutrino energy loss rates      Ephemeris routines      Fermi-Dirac functions      Polyhedra volume      Plane - cube intersection      Coating an ellipsoid      Nuclear reaction networks      Nuclear statistical equilibrium      Laminar deflagrations      CJ detonations      ZND detonations      Fitting to conic sections      Unusual linear algebra      Derivatives on uneven grids      Pentadiagonal solver      Quadratics, Cubics, Quartics      Supernova light curves      Exact Riemann solutions      1D PPM hydrodynamics      Hydrodynamic test cases      Galactic chemical evolution      Universal two-body problem      Circular and elliptical 3 body      The pendulum      Phyllotaxis      MESA      MESA-Web      FLASH      Zingale's software      Brown's dStar      GR1D code      Iliadis' STARLIB database      Herwig's NuGRID      Meyer's NetNuc AAS Journals    2025 AAS YouTube    2025 AAS Peer Review Workshops 2025 ASU Energy in Everyday Life 2025 MESA Classroom Other Stuff:    Bicycle Adventures    Illustrations    Presentations Contact: F.X.Timmes my one page vitae, full vitae, research statement, and teaching statement.	The tool sneut5.tbz implements the analytic fitting formulas of Itoh et al. 1996 for thermal neutrino losses. In addition, the tool also returns the neutrino loss rate and its derivatives with respect to its input values: temperature, density, and the composition variables abar and zbar. 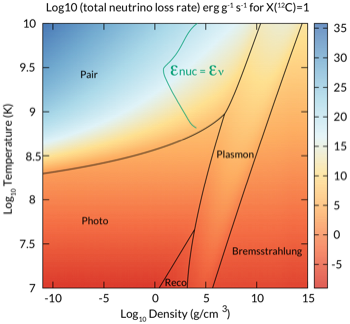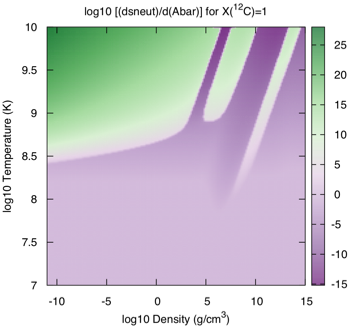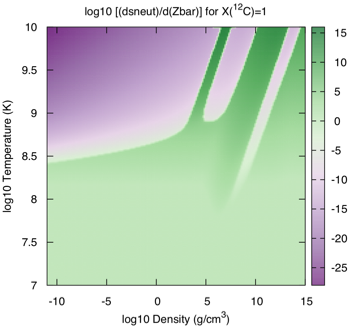As shown in the first figure above, the thermal neutrino losses has several components: ⚬ Pair production: $e^+ + e^- \rightarrow \nu_e + {\bar \nu}_e$ dominates in massive stars, where $kT \ge 0.1 \ m_ec^2$ especially for $T_9 > 0.5$. 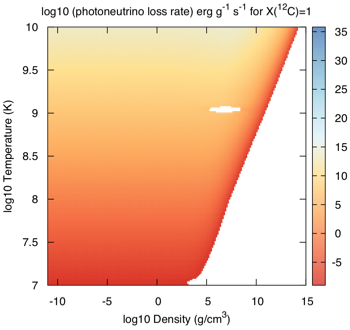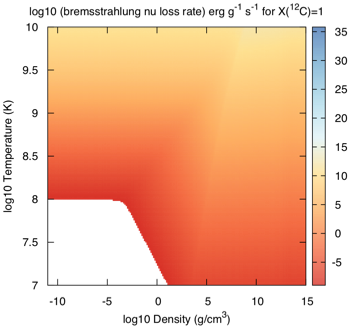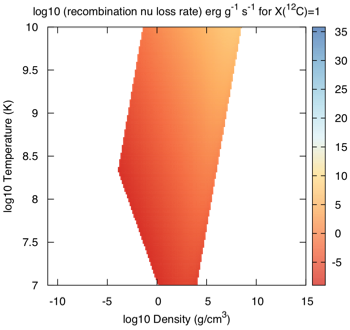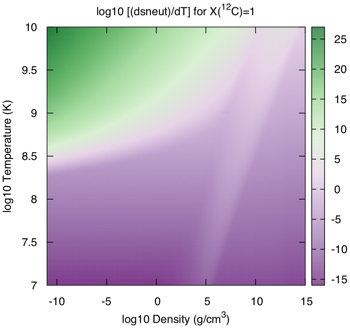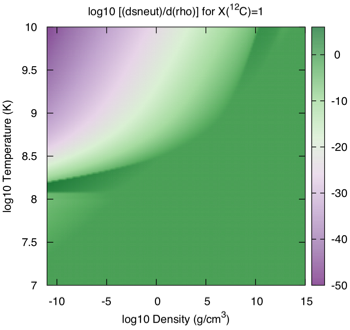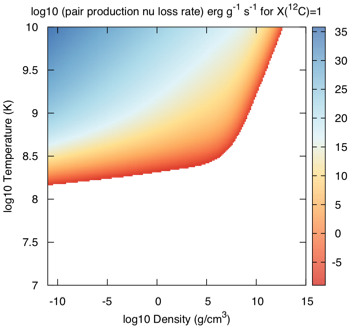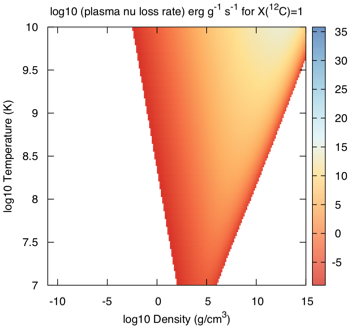⚬ Photoneutrino: $e^{\pm} + \gamma \rightarrow e^{\pm} + \nu + \bar{ \nu}_e$ ⚬ Plasmon neutrino: $\gamma_{{\rm plasmon}} \rightarrow \nu_e + \bar{ \nu}_e$ ⚬ Bremsstrahlung: $e^- + A^Z \rightarrow e^- + A^Z + \nu_e + \bar{\nu}_e$ ⚬ Recombination: $e^-_{\rm continuum} \rightarrow e^-_{\rm bound} + \nu_e + \bar{ \nu}_e$ Here is how the Itoh et al expressions look in the ρ-T plane for pure carbon:
	Please cite the relevant references if you publish a piece of work that use these codes, pieces of these codes, or modified versions of them. Offer co-authorship as appropriate.